Levels and Statistics

This section provides an overview of how to determine and set signal levels using the Signal class and its stats property.

Getting Signal Statistics

All level calculations and statistics are accessed through the .stats property, which returns a SignalStats object. This provides convenient access to common metrics, calculated per channel.

Let’s create a noise signal to demonstrate:

>>> import audiotoolbox as audio
>>> import numpy as np
>>>
>>> noise = audio.Signal(n_channels=2, duration=1, fs=48000).add_noise('pink')

The following properties are available:

.stats.rms: The Root-Mean-Square level of the signal.
.stats.dbspl: The level in dB Sound Pressure Level (SPL), assuming
the signal values are pressure in Pascals relative to 20 µPa.
.stats.dbfs: The level in dB Full Scale, where 0 dBFS is a sine
wave with an amplitude of 1.
.stats.dba and .stats.dbc: A- and C-weighted SPL.
.stats.crest_factor: The ratio of the peak amplitude to the RMS value.
.stats.mean: The mean value of the signal.
.stats.var: The variance of the signal.

>>> # Get various level and statistical properties
>>> print(f"Mean: {noise.stats.mean}")
Mean: Signal([-2.4e-17, -2.4e-17])
>>>
>>> print(f"Level in dBFS: {noise.stats.dbfs}")
Level in dBFS: Signal([3.01, 3.01])
>>>
>>> print(f"A-weighted SPL: {noise.stats.dba}")
A-weighted SPL: Signal([89.10, 89.10])

Setting and Normalizing Levels

To change a signal’s level, use the methods directly available on the Signal object.

# Normalize the signal to 70 dB SPL
noise.set_dbspl(70)

# The .stats.dbspl property will now reflect this new level
print(f"New SPL: {noise.stats.dbspl}")
# New SPL: Signal([70., 70.])

# Normalize the signal to -6 dBFS
noise.set_dbfs(-6)
print(f"New dBFS: {noise.stats.dbfs}")
# New dBFS: Signal([-6., -6.])

Octave-Band Levels

It is also possible to get the octave-band or fractional-octave-band levels of a signal using octave_band_levels().

import audiotoolbox as audio
import numpy as np
import matplotlib.pyplot as plt

# Create a pink noise signal
noise = audio.Signal(1, duration=5, fs=48000).add_noise('white')

# Calculate octave-band levels
fc, levels = noise.stats.octave_band_levels(oct_fraction=3)

base_value = -50
# Plot the results
plt.figure(figsize=(8, 5))
plt.bar(np.arange(len(fc)), levels -base_value, tick_label=np.round(fc).astype(int), bottom=base_value)
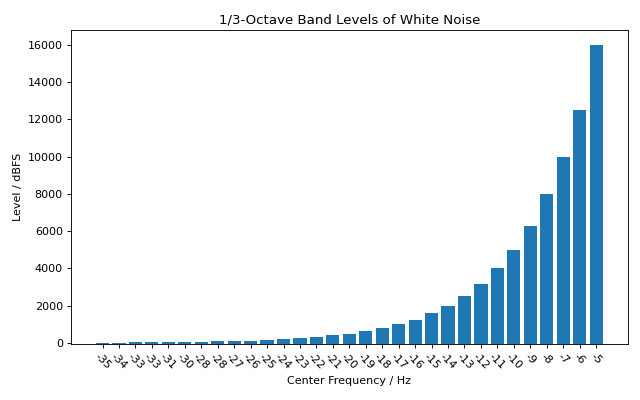
plt.title('1/3-Octave Band Levels of White Noise')
plt.xlabel('Center Frequency / Hz')
plt.ylabel('Level / dBFS')
plt.xticks(rotation=-45)
plt.tight_layout()
plt.show()

(Source code, png, hires.png, pdf)